Pourquoi 97 ?

Je propose chaque année à mes élèves de 4^e, durant les vacances de la Toussaint, un devoir à la maison autour du N.I.R.¹ Ils y doivent obtenir le N.I.R. d’un membre de leur famille, montrer qu’ils sont capables d’en vérifier la clé puis montrer que la modification du N.I.R. sur un seul chiffre est repérée par une variation de la clé.

La première question de ce devoir est: « À votre avis, quel est la particularité du nombre 97 qui justifie qu’on l’utilise comme diviseur dans le calcul de la clé ? » et une réponse suffisante à leur niveau de compétence est « 97 est le plus grand nombre premier inférieur à 100, il permet donc d’obtenir un très grand nombre de clés différentes et de corriger les N.I.R comportant une erreur.».

Pour la première fois en 2024, une — très bonne — élève a répondu: « 97 est le plus grand nombre premier inférieur à 100, il permet donc d’obtenir le plus grand nombre de clés différentes, même si je suis incapable de le démontrer. » Dans les jours suivants, j’ai rencontré le père de cette élève qui m’a avoué s’être posé le problème et ne pas avoir réussi à démontrer que la primalité de 97 ait un intérêt véritable, ce qui pourrait signifier que 99, par exemple, augmenterait le nombre de clés différentes possibles. J’ai été incapable de le lui démontrer à la volée ce qui m’a grandement intrigué.

Mes recherches sur une explication historique à ce choix, apparemment réalisé à la fin des années 70 dans le cadre de l’installation des premiers ordinateurs dans l’administration française, ce sont révélées vaines. Même l’I.N.S.E.E., qui a hérité en 1982²de la gestion du N.I.R., ne propose à ma connaissance dans ses archives aucune trace des modalités de création de ce protocole de calcul de clé. Par ailleurs, une recherche en ligne — prompte a être effectuée par des élèves peu scrupuleux et désireux de se débarrasser de mon devoir — remonte invariablement les mêmes arguments incomplets, voire faux. En l’absence de réponses satisfaisantes, j’ai donc décidé de reprendre le problème à sa source.

Cahier des charges pour une clé

Dans la France de la fin des années 70, les compétences nécessaires à la réalisation des programmes informatiques sont le monopole quasi-exclusif des ingénieur(e)s issu(e)s de nos grandes écoles, seul(e)s à posséder à la fois de très solides compétences mathématiques et une conscience précise des limitations techniques des ordinateurs disponibles.

Nous ne pouvons qu’imaginer ce qu’a pu être le cahier des charges établi par l’équipe chargée d’implémenter un système de clé de vérification du N.I.R.:

la clé doit être simple pour être comprise par l’opérateur final, supposé néophyte en informatique,
la clé doit nécessiter le moins d’allocation mémoire possible, mais ne doit pas être nulle pour ne pas être assimilée à une absence de clé,
la clé doit être obtenue simplement à partir des 13 caractères du N.I.R, par un calcul portant sur des nombres entiers pour éviter les erreurs informatiques liées aux virgules flottantes,
la clé doit être la plus diverse possible, pour être la plus discriminante possible,
la clé doit permettre de mettre en évidence et d’alerter l’opérateur sur les erreurs de saisie les plus courantes, à savoir la mauvaise saisie d’un caractère ou la permutation de deux caractères consécutifs.

Les trois premières contraintes mènent presque naturellement — en tous cas dans l’esprit d’un ingénieur — à une clé codée sur deux chiffres. La troisième oriente l’esprit mathématicien vers l’emploi de l’arithmétique, en l’occurence de la division euclidienne, tandis que la quatrième mène à l’emploi d’une division par le nombre le plus grand possible fournissant un reste assurément à deux chiffres.

En l’état, et abstraction faite d’une division par 100 sans intérêt puisque son reste consiste en les deux derniers chiffres du N.I.R., le choix d’une division euclidienne par 99 fournissant 99 restes allant de 0 à 98, puis d’une différence à 99 fournissant 99 clés allant de 1 à 99 semble le plus opportun.

Pourtant les ingénieur(e)s en charge du projet ont choisi 97. Est-ce la cinquième contrainte qui a guidé ce choix, ou une autre contrainte non-évoquée ici, ou même la simple beauté esthétique du choix d’un nombre premier ?

Nous allons montrer ici que la cinquième contrainte ne favorise pas 97 au détriment de 99 et nous ferons alors des conjectures sur l’éventuelle supériorité de ce choix, pour des raisons que nous chercherons alors à déterminer.

Résultats comparés

La relation d’inversion qui permet de calculer la clé à partir du modulo étant bijective, nous ne nous intéresserons désormais plus dans la suite de notre recherche qu’au résultat du modulo. Par ailleurs, nous ferons toujours l’hypothèse qu’il n’y a pas d’erreur sur la clé, donc sur le modulo.

Ventilation des restes

Nous allons opérer les simplifications suivantes qui ne nuisent pas à la généralité du propos, en commençant par nous limiter aux naissances en France métropolitaine:

Les 3 derniers chiffres, qui représentent le numéro d’ordre de la naissance, vont de $1$ à $999$. Ils formeront donc le nombre $1\leq o \leq 999$
Les trois chiffres suivant, qui identifient la commune de naissance, vont de $1$ à $999$. Ils formeront donc le nombre $1\leq v \leq 999$
Les deux chiffres suivant, qui identifient le département de naissance, vont de $1$ à $95$. Ils formeront donc le nombre $1\leq d \leq 95$
Les deux chiffres suivant, qui identifient le mois de naissance, vont de $1$ à $12$. Ils formeront donc le nombre $1\leq m \leq 12$
Les deux chiffres suivant, qui identifient l’année de naissance, vont de $0$ à $99$. Ils formeront donc le nombre $0\leq y \leq 99$
Le dernier chiffre représente le genre, il est noté $1\leq g\leq 2 $

Ainsi, le N.I.R formé peut s’écrire:

$$N=g\times 10^{12}+y\times 10^{10}+m\times 10^8+d\times 10^6+v\times 10^3+o$$

Partant, remarquons que $10^2=100\equiv 1\;[99]$ et pour tout entier $k$ nous avons:

$$10^{2k}=\left(10^2\right)^k\equiv 1\;[99] \qquad 10^{2k+1}=\left(10^2\right)^k\times 10\equiv 10\;[99]$$

Il vient alors:

$$N\equiv g+y+m+d+10\,v+o\;[99]$$

De même, notons que:

$$10^3\equiv 30\,[97] \qquad 10^6\equiv 27\;[97] \qquad 10^8\equiv 81\;[97]$$

$$10^{10}\equiv 49\;[97] \qquad 10^{12}\equiv 50\;[97]$$

Il vient alors:

$$ N\equiv 50 \times g+49 \times y+81 \times m+27 \times d+30\,v+o\;[97] $$

Remarquons enfin que $g$ contribue à hauteur de 1 ou 2 au modulo 99 tandis qu’il contribue à hauteur de 50 ou 3 au modulo 97, c’est à dire qu’il opère dans les deux cas une simple translation des restes obtenu sans lui. Nous nous passerons donc de $g$ dans le programme en Python chargé de calculer les effectifs de tous les restes possibles, ce qui divisera le temps de calcul par 2 au moins.

Notre corpus est donc constitué de $999\times 999\times 95 \times 12\times 99 $ nombres distincts non-consécutifs et les résultats — fournis en Annexe 2 et obtenus après environ 15 h de calculs par le programme fourni en Annexe 1 — sont probants: il n’y a pas de restes grandement favorisés par l’un ou l’autre des deux modulos et tout au plus constatons nous une très légère variation entre les restes les plus courants et les moins courants.

Nous concluons donc que le choix d’un modulo 97 ou 99 n’a pas d’impact significatif sur la distribution des restes: nous sommes quasiment dans une situation d’équirépartition dans les deux cas.

Erreur de saisie sur un caractère

Voici en appui le tableau des restes des divisions des puissances de $10$ dans les deux modulos que nous cherchons à comparer:

12	11	10	9	8	7	$n$
1	10	1	10	1	10	$10^n\;[99]$
50	5	49	34	81	76	$10^n\;[97]$

6	5	4	3	2	1	0	$n$
1	10	1	10	1	10	1	$10^n\;[99]$
27	90	9	30	3	10	1	$10^n\;[97]$

Imaginons qu’un opérateur se trompe, dans sa saisie, en remplaçant un chiffre $a$ du N.I.R. par le chiffre $b$, tous deux compris entre 0 et 9.

Au modulo 99:
- Si le chiffre mal saisi est de rang pair: $$ a\times 10^{2k}\equiv b\times 10^{2k}\;[99] \implies a\equiv b \;[99] \implies a=b $$
- Si le chiffre mal saisi est de rang impair: $$a\times 10^{2k+1}\equiv b\times 10^{2k+1}\;[99] \implies 10\,a\equiv 10\,b \;[99] \implies 10(a-b)\equiv 0\;[99]$$
  Or 99 est premier avec 10 donc d’après le théorème de Gauss ³ 99 divise $(a-b)$, lui-même compris entre $-9$ et $9$. La seule possibilité est encore $a=b$
Au modulo 97:
Nous constatons que tous les restes sont différents et tous premiers avec 97 puisqu’il est lui-même premier.
Notons $10^k\equiv r_k\;[97]$ et nous avons alors, pour tout $k$ avec $0\leq k\leq 12$:
$$a\times 10^k\equiv b\times 10^k\;[97] \implies a\times r_k\equiv b\times r_k \;[97] \implies r_k(a-b)\equiv 0\;[97]$$
À nouveau,97 étant premier avec $r_k$ le théorème de Gauss nous dit que 97 divise $(a-b)$ ce qui n’est possible que si $a=b$

Par contraposition, dans les deux cas, toute modification d’un unique chiffre entraine une modification du reste, donc de la clé. L’opérateur n’aura donc qu’à relire le N.I.R. pour voir où il a commis son erreur et pourra la corriger.

Erreur de permutation entre deux caractères consécutifs

Notons $a_k$ pour $0\leq k\leq 11$, le $k$-ième chiffre du N.I.R. en partant de la droite

Au modulo 99 nous avons:
$$\begin{aligned} &10^{k+1}\,a_{k+1}+10^k\,a_k \equiv 10^{k+1}\,a_{k}+10^k\,a_{k+1}\;[99]\\ &\implies 10^k(10\,a_{k+1}+a_k-10\,a_k-a_{k+1})\equiv 0\;[99]\\ &\implies 10^k\times 9(a_{k+1}-a_k)\equiv 0\;[99] \end{aligned}$$
Ainsi si $k$ est pair nous avons $9(a_{k+1}-a_k)\equiv 0\;[99]$ et sinon nous avons $90(a_{k+1}-a_k)\equiv 0\;[99]$ et le théorème de Gauss ne permet pas de conclure puisque 9 n’est premier ni avec 9 ni avec 90.
Au modulo 97 nous avons:
$$\begin{aligned}&10^{k+1}\,a_{k+1}+10^k\,a_k \equiv 10^{k+1}\,a_{k}+10^k\,a_{k+1}\;[97]\\ &\implies r_{k+1}\,a_{k+1}+r_{k}\,a_{k}\equiv r_{k+1}\,a_{k}+r_{k}\,a_{k+1}\;[97]\\ &\implies (r_{k+1}-r_k)(a_{k+1}-a_k)\equiv 0\;[97] \end{aligned}$$
Or nous avons vu dans notre tableau des restes qu’ils sont tous compris entre 1 et 90, donc nous aurons $-89\leq r_{k+1}-r_k\leq 89 $.
Ainsi 97 premier sera premier avec $r_{k+1}-r_k$ et d’après le théorème de Gauss 97 divise $a_{k+1}-a_k$ ce qui n’est possible que si $a_{k+1}=a_k$ et l’inversion n’en est plus vraiment une!

Il semblerait donc que 97, contrairement à 99, réussisse à mettre en évidence la permutation de caractères consécutifs dans une saisie, une erreur de saisie unanimement reconnue comme courante.

En théorie d’accord, mais en pratique ?

Nous pourrions nous en tenir là, acter la supériorité théorique de 97 dans la détermination des erreurs de permutations lors de la saisie et considérer que cette supériorité est la raison pour laquelle l’équipe chargée de mettre en place cette méthode a fait ce choix.

Nous fournissons cependant, en Annexe 3, deux tableaux obtenus avec un simple tableur. Ils fournissent les résultats au modulo 99 de la permutation de deux chiffres consécutifs d’un N.I.R. dans les deux cas possibles, à savoir entre rang pair et impair et réciproquement.

Nous y constatons que les seuls 0 obtenus sont sur les diagonales, à savoir quand la permutation est sans intérêt puisqu’elle concerne deux chiffres identiques. Dans tous les autres cas, cette permutation produit une variation du reste au modulo 99.

Nous nous refusons à croire que les ingénieurs en charge du projet n’avaient pas constaté ce résultat, qui invalide la supériorité théorique de 97.

Notre quête continue…

Le maillon faible: l’assuré

Il nous faut nous souvenir des circonstances dans lesquelles s’opère la saisie du N.I.R. sur un ordinateur: jusqu’à la création de la Carte Vitale, et encore aujourd’hui dans certaines circonstances exceptionnelles, le N.I.R. était écrit à la main par l’assuré sur sa feuille de soins, feuille envoyée par courrier à la CPAM et reçue par ses employés qui devaient en effectuer la saisie.

Se pourrait-il que 97 révèle sa supériorité dans les cas où c’est l’assuré lui-même qui commet une erreur, en permettant éventuellement de retrouver cette erreur et de la corriger ?

Pour vérifier cette hypothèse, nous fournissons en Annexe 4 deux tableaux de tous les restes possibles aux modulos 97 et 99 de $a_k \times 10^k$ avec $k$ compris entre $0$ et $12$.

Erreur-type 1: un chiffre précis est illisible

Nous constatons sans surprise que, dans les deux tableaux, sur une ligne donnée, tous les restes sont différents. Les deux modulos permettent donc de remplacer le chiffre illisible à coup sûr.

Prenons pour exemple le N.I.R suivant: 2.43.08.03.108.441

Au modulo 97 son reste est 21
Imaginons que le cinquième chiffre en partant de la gauche (c’est à dire pour $k=8$) soit illisible.
Nous pouvons remplacer ce chiffre par 0 et calculer le nouveau reste:
$$2430003108441 \equiv 52\;[97] \quad \text{et} \quad 21-52=-31\equiv 66\;[97]$$
Dans notre tableau, à la ligne $k=8$, le nombre 66 apparait uniquement à la colonne indiquant le chiffre 8, qui était illisible et a été retrouvé.
Au modulo 99 son reste est 92
Imaginons que le septième chiffre en partant de la gauche (c’est à dire pour $k=6$) soit illisible.
Nous pouvons remplacer ce chiffre par $0$ et calculer le nouveau reste:
$$2430800108441 \equiv 89\;[99] \quad \text{et} \quad 92-89=3\equiv 3\;[97]$$
Dans notre tableau, à la ligne $k=6$, le nombre 3 apparait uniquement à la colonne indiquant le chiffre 3, qui était illisible et a été retrouvé.

Sans surprise, les deux modulos sont tout aussi efficaces pour corriger ce type d’erreur, pour la simple raison que tous les restes sont différents sur une ligne donnée connue à l’avance.

Erreur-type 2: un unique chiffre est erroné

Les choses se compliquent désormais car nous ne savons pas à quel rang $k$ se situe l’erreur.

Au modulo 99:
Nous avons montré et nous voyons clairement dans le tableau de l’Annexe 4 qu’il n’y a que deux restes possibles différents dans chaque colonne. Ce qui signifie que si notre méthode précédente mettait en évidence une erreur par exemple de 7, nous ne saurions attribuer cette erreur à un chiffre précis dans la mesure où 7 apparait à la colonne 7 sur tous les chiffres de rang pair, ce qui donnerait 6 corrections possibles.
Il est donc systématiquement impossible de corriger une erreur de ce type avec un modulo 99.
Au modulo 97:
Tous les restes sont différents dans une colonne donnée, ce qui laisse espérer une correction possible. Malheureusement, ce ne sera pas toujours le cas.
En effet constatons les résultats suivants:
$$\begin{aligned}\forall n\in\mathbb{N}:\qquad 10^{n+4}-3\times 10^{n+2}=10^{n+2}(10^2-3)=97\times 10^{n+2}&\equiv 0\;[97]\\ 3\times 10^{n+2}-9\times 10^n=3\times 10^n(10^2-3)=3\times 10^n\times 97&\equiv 0\;[97]\\ 9\times 10^{n+7}-5\times 10^n=10^n(9\times 10^7-5)\equiv 10^n(9\times 76-5)&\equiv 0\;[97] \end{aligned}$$
Ce qui signifie que les colonnes 1,3,5 et 9 fournissent des résultats similaires simplement décalés, comme nous pouvons le constater dans le tableau.
De même:
$$\begin{aligned}\forall n\in\mathbb{N}:\qquad 2\times 10^{n+2}-6\times 10^n=2\times 10^n(100-3)&\equiv 0\;[97] \end{aligned}$$
Ce qui signifie que les colonnes 2 et 6 fournissent des résultats similaires simplement décalés, comme nous pouvons également le constater dans le tableau.
Nous savons donc que la correction sera parfois possible, comme nous pouvons le montrer sur les deux exemples suivants, basés sur le N.I.R. correct 1.69.12.75.112.447 dont les reste est 50 au modulo 97
- Exemple 1:
  L’assuré s’est trompé et a écrit 1.69.12.79.112.447 qui renvoie un reste valant 61.
  Or $50-61=-11\equiv 86\;[97] $ tandis que $61-50=11\equiv 11\;[97] $
  Dans le tableau, nous constatons que 86 n’apparait pas mais que 11 apparait une seule fois, à la ligne de rang 6 et sur la colonne du chiffre 4.
  Il faut donc soustraire 4 au chiffre de rang 6 et le 9 erroné redevient un 5: le N.I.R a été corrigé.
- Exemple 2:
  L’assuré s’est trompé et a écrit 1.69.11.75.112.447 qui renvoie un reste valant 66.
  Or $50-66=-16\equiv 81\;[97]$ tandis que $66-50=16\equiv 16\;[97] $
  Dans le tableau, nous constatons que 16 apparait une fois, à la ligne de rang 3 et sur la colonne du chiffre 7. Il faudrait donc soustraire 7 au chiffre de rang 3, ce qui est impossible en l’occurence.
  Quant à 81, il apparait à 3 reprises:
  - À la ligne de rang 6 au chiffre 3, ce que nous corrigeons en ajoutant 3 au rang 6 pour donner le N.I.R. 1.69.11.78.112.447 qui est admissible mais faux,
  - À la ligne de rang 4 au chiffre 9, ce que nous corrigeons en ajoutant 9 au rang 4, ce qui n’est pas possible en l’occurence,
  - À la ligne de rang 8 au chiffre 1, ce que nous corrigeons en ajoutant 1 au rang 8 pour donner, cette fois-ci, le N.I.R. correct.

En réalité, le N.I.R. ne sera corrigé à coup sûr que lorsque la différence recherchée sera unique dans le tableau. Nous proposons en Annexe 5 une compilation du premier tableau de l’Annexe 4, regroupant le nombre d’occurrences de chacun des 97 restes potentiels et nous constatons qu’un reste n’apparait qu’une fois dans $\frac{34}{62}\approx 55\,\% $ des cas, ce qui est un résultat pas très satisfaisant.

Erreur-type 3: permutation de deux chiffres consécutifs

Il est ici extrêmement difficile de se faire une idée précise de notre capacité à corriger à la main une permutation de deux chiffres consécutifs.

Au modulo 99:
Force est de constater, à l’aide des deux tableaux de l’Annexe 3, que les restes au modulo 99 se répètent beaucoup trop pour être caractéristiques d’un permutation précise.
Par exemple, le reste $90$ apparait au-dessus de la diagonale du premier tableau et en dessous de la diagonale du second, c’est à dire rien que $18$ fois dans nos deux tableaux, soit potentiellement $6\times 18$ fois en tout ! Autant dire qu’il est très improbable de caractériser une permutation précise avec ce modulo.
Au modulo 97:
Nous nous sommes épargnés la fabrication et la restitution des 12 tableaux présentant les restes au modulo 97 des permutations des deux chiffres consécutifs à toutes les puissances de 10. Un rapide programme en Python fourni en Annexe 6 nous renvoie cependant des résultats intéressants:
- Sans surprise, le reste nul, qui caractérise la permutation de deux chiffres identiques, apparait 120 fois, c’est à dire sur la diagonale de chacun des 12 tableaux,
- Aucun reste n’apparait qu’une seule fois, ce qui signifie qu’aucun reste n’est — malheureusement — caractéristique d’une unique permutation,
- Les restes qui apparaissent plus de 9 fois sont présents dans des tableaux différents, donc très peu représentatifs,
- Les restes qui apparaissent moins de $9$ fois n’apparaissent que dans un unique tableau: ils sont donc plus caractéristiques et peuvent éventuellement permettre de retrouver une erreur.

Quoi qu’il en soit, nous constatons que le modulo 97 n’est pas significativement plus efficace que 99 pour corriger une erreur de permutation.

Synthèse des résultats

Nous pouvons désormais faire la synthèse de tous nos résultats comparés et exposer leurs capacités de corrections relatives:

Modulo	97	99
Erreur sur la saisie d’un chiffre	À coup sûr	À coup sûr
Erreur de permutation à la saisie	À coup sûr	À coup sûr
Un chiffre illisible	À coup sûr	À coup sûr
Erreur sur un chiffre quelconque	Dans 55% des cas	Impossible
Permutation de deux chiffres consécutifs	Très improbable	Impossible

En fin de compte, nos hypothèses sont invalidées: 97 et 99 sont tout aussi efficaces à mettre en évidence une erreur de saisie de l’opérateur ou un chiffre illisible, mais 97 ne se révèle pas capable de corriger systématiquement une erreur sur un chiffre quelconque ou une erreur de permutation. Ses capacités partielles se sont-elles révélées suffisantes dans l’esprit des créateurs du protocole ? Nous ne le saurons probablement jamais…

En conclusion, nous proposons en Annexe 7 un programme en Python qui, sous forme d’une fonction demandant comme argument un N.I.R erroné et la clé du N.I.R. correct correspondant, renvoie la liste de tous les N.I.R. susceptibles de convenir. Il permettra au lecteur curieux de vérifier les exemples fournis ici et de tester ses propres exemples, s’assurant ainsi que les erreurs courantes ne sont pas repérées à coup sûr.

Il va sans dire que je suis preneur de toute remarque constructive sur cet article: je vous invite donc à vous manifester dans les commentaires tout en bas de cette page si vous pensez relever une erreur dans mes calculs, avoir une réponse à cette interrogation ou des précisions à apporter !

Annexe 1 — Ventilation des restes aux modulos 97 et 99

ventilation_97 = [[i,0] for i in range(97)]
ventilation_99 = [[i,0] for i in range(99)]

for year in range(100):
    for mois in range(1,13):
        for dep in range(1,96):
            for ville in range(1,1000):
                for ordre in range(1,1000):
                    reste_97 = (49*year+81*mois+27*dep+30*ville+ordre) % 97 
                    reste_99 = (year+mois+dep+10*ville+ordre) %99 
                    ventilation_97[reste_97][1] += 1
                    ventilation_99[reste_99][1] += 1

#Tris à bulles
n = len(ventilation_97)
for i in range(n):
    for j in range(0, n-i-1):
        if ventilation_97[j][1] > ventilation_97[j+1][1] :
            ventilation_97[j], ventilation_97[j+1] = ventilation_97[j+1], ventilation_97[j]

n = len(ventilation_99)
for i in range(n):
    for j in range(0, n-i-1):
        if ventilation_99[j][1] > ventilation_99[j+1][1] :
            ventilation_99[j], ventilation_99[j+1] = ventilation_99[j+1], ventilation_99[j]

print(ventilation_97)
print(ventilation_99)

Annexe 2 — Résultats de la ventilation des restes

Effectifs des restes au modulo 97 classés dans l’ordre croissant:

[[7, 11729082], [9, 11729082], [23, 11729082], [25, 11729082], [39, 11729082], [41, 11729082], [42, 11729082], [55, 11729082], [58, 11729082], [71, 11729082], [72, 11729082], [74, 11729082], [88, 11729082], [90, 11729082], [0, 11729083], [5, 11729083], [11, 11729083], [16, 11729083], [21, 11729083], [26, 11729083], [27, 11729083], [28, 11729083], [32, 11729083], [37, 11729083], [44, 11729083], [48, 11729083], [49, 11729083], [53, 11729083], [56, 11729083], [57, 11729083], [60, 11729083], [64, 11729083], [65, 11729083], [69, 11729083], [76, 11729083], [81, 11729083], [85, 11729083], [86, 11729083], [87, 11729083], [92, 11729083], [2, 11729084], [4, 11729084], [6, 11729084], [8, 11729084], [10, 11729084], [12, 11729084], [14, 11729084], [18, 11729084], [22, 11729084], [24, 11729084], [33, 11729084], [34, 11729084], [38, 11729084], [40, 11729084], [43, 11729084], [54, 11729084], [59, 11729084], [70, 11729084], [73, 11729084], [75, 11729084], [79, 11729084], [80, 11729084], [89, 11729084], [91, 11729084], [95, 11729084], [1, 11729085], [15, 11729085], [17, 11729085], [19, 11729085], [20, 11729085], [30, 11729085], [35, 11729085], [46, 11729085], [50, 11729085], [51, 11729085], [62, 11729085], [63, 11729085], [67, 11729085], [78, 11729085], [83, 11729085], [93, 11729085], [94, 11729085], [96, 11729085], [3, 11729086], [13, 11729086], [29, 11729086], [31, 11729086], [36, 11729086], [45, 11729086], [47, 11729086], [52, 11729086], [61, 11729086], [66, 11729086], [68, 11729086], [77, 11729086], [82, 11729086], [84, 11729086]]

Effectifs des restes au modulo 99 classés dans l’ordre croissant:

[[23, 11492128], [24, 11492128], [25, 11492128], [26, 11492128], [27, 11492128], [33, 11492128], [34, 11492128], [35, 11492128], [36, 11492128], [37, 11492128], [43, 11492128], [44, 11492128], [45, 11492128], [46, 11492128], [47, 11492128], [53, 11492128], [54, 11492128], [55, 11492128], [56, 11492128], [57, 11492128], [63, 11492128], [64, 11492128], [65, 11492128], [66, 11492128], [67, 11492128], [73, 11492128], [74, 11492128], [75, 11492128], [76, 11492128], [77, 11492128], [83, 11492128], [84, 11492128], [85, 11492128], [86, 11492128], [87, 11492128], [93, 11492128], [94, 11492128], [95, 11492128], [96, 11492128], [97, 11492128], [22, 11492129], [28, 11492129], [32, 11492129], [38, 11492129], [42, 11492129], [48, 11492129], [52, 11492129], [58, 11492129], [62, 11492129], [68, 11492129], [72, 11492129], [78, 11492129], [82, 11492129], [88, 11492129], [92, 11492129], [98, 11492129], [29, 11492130], [30, 11492130], [31, 11492130], [39, 11492130], [40, 11492130], [41, 11492130], [49, 11492130], [50, 11492130], [51, 11492130], [59, 11492130], [60, 11492130], [61, 11492130], [69, 11492130], [70, 11492130], [71, 11492130], [79, 11492130], [80, 11492130], [81, 11492130], [89, 11492130], [90, 11492130], [91, 11492130], [0, 11492131], [21, 11492131], [1, 11492133], [20, 11492133], [2, 11492136], [19, 11492136], [3, 11492139], [18, 11492139], [4, 11492142], [17, 11492142], [5, 11492146], [16, 11492146], [6, 11492150], [15, 11492150], [7, 11492154], [14, 11492154], [8, 11492158], [13, 11492158], [9, 11492161], [12, 11492161], [10, 11492163], [11, 11492163]]

Annexe 3 — Permutations de chiffres consécutifs au modulo 99

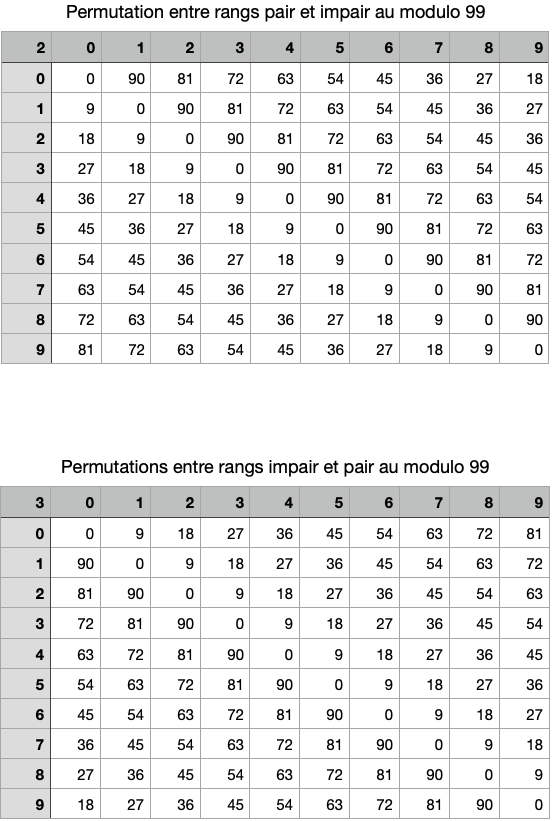
Exemple du premier tableau: si nous permutons un 4 situé à un rang pair avec un 2 situé à sa gauche, nous allons à la colonne 4, ligne 2, pour constater que cette permutation génère une différence de modulo de 81.

Exemple du second tableau: si nous permutons un 7 situé à un rang impair avec un 3 situé à sa gauche, nous allons à la colonne 7, ligne 3, pour constater que cette permutation génère une différence de modulo de 36.

Annexe 4 — Restes possibles aux modulos 97 et 99

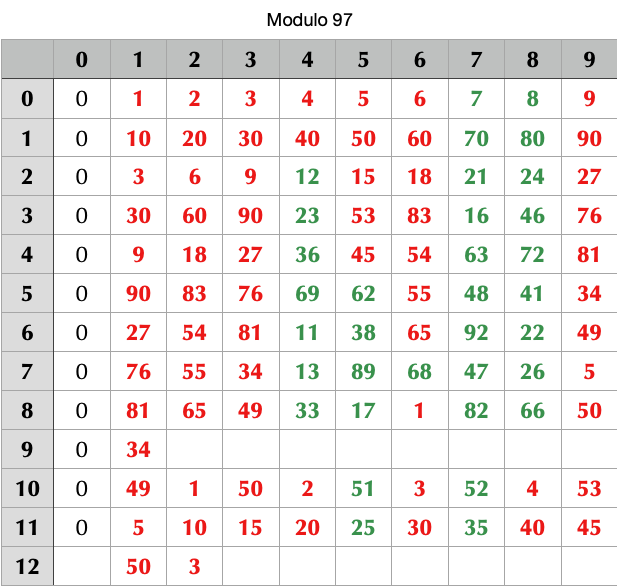
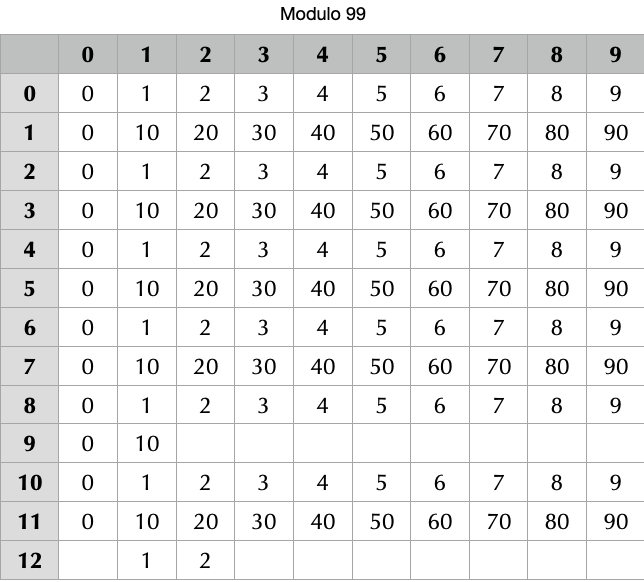
Exemple du premier tableau: le chiffre 5 placé au rang 7 génère un reste de 89 au modulo 97

Exemple du second tableau: le chiffre 4 placé au rang 11 génère un reste de 40 au modulo 99

Annexe 5 — Effectifs des restes possibles au modulo 97

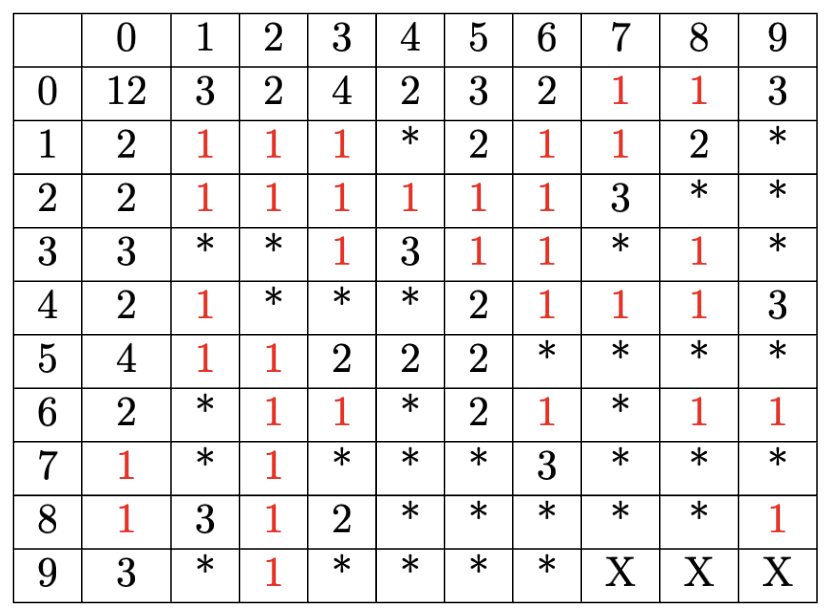
Exemples:

le reste 76 est lisible à la ligne 7 colonne 6: il apparait 3 fois,
le reste 41 est lisible à la ligne 4 colonne 1: il n’apparait qu’une fois,
le reste 87 est lisible à la ligne 8 colonne 7: il n’apparait jamais.

Nous remarquons que:

Sur les 97 restes possibles, 35 n’apparaitrons jamais.
Ils sont marqués par une étoile et laissent donc 62 restes atteignables.
Sur les 62 restes atteignables, 34 n’apparaissent qu’une seule fois.
Ils sont marqués en rouge et permettent de corriger le N.I.R. à coup sûr.

Annexe 6 — Effectifs des restes possibles des permutations au modulo 97

effectifs = [[i,0] for i in range(97)]
for k in range(12):
    for a in range(10):
        for b in range(10):
            r = (9*10**k*(a-b))%97
            effectifs[r][1] += 1
print(effectifs)

Ce programme renvoie la liste suivante:

[[0, 120], [1, 12], [2, 6], [3, 12], [4, 2], [5, 20], [6, 6], [7, 21], [8, 9], [9, 21], [10, 12], [11, 6], [12, 2], [13, 6], [14, 14], [15, 20], [16, 17], [17, 9], [18, 14], [19, 2], [20, 6], [21, 20], [22, 7], [23, 2], [24, 8], [25, 7], [26, 7], [27, 20], [28, 8], [29, 12], [30, 12], [31, 7], [32, 12], [33, 6], [34, 20], [35, 16], [36, 8], [37, 6], [38, 16], [39, 6], [40, 2], [41, 7], [42, 12], [43, 12], [44, 20], [45, 25], [46, 5], [47, 20], [48, 20], [49, 20], [50, 20], [51, 5], [52, 25], [53, 20], [54, 12], [55, 12], [56, 7], [57, 2], [58, 6], [59, 16], [60, 6], [61, 8], [62, 16], [63, 20], [64, 6], [65, 12], [66, 7], [67, 12], [68, 12], [69, 8], [70, 20], [71, 7], [72, 7], [73, 8], [74, 2], [75, 7], [76, 20], [77, 6], [78, 2], [79, 14], [80, 9], [81, 17], [82, 20], [83, 14], [84, 6], [85, 2], [86, 6], [87, 12], [88, 21], [89, 9], [90, 21], [91, 6], [92, 20], [93, 2], [94, 12], [95, 6], [96, 12]]