
Le geek en moi s’était réjoui, en 2021, du passage à l’écran d’un univers qui avait profondément marqué sa jeunesse, celui de la saga « Fondation » d’Isaac Asimov. La première saison, très réussie du point de vue de la réalisation, m’avait cependant intrigué tant elle me semblait éloignée de mon souvenir, et pour cause: elle s’appuyait principalement sur, et brodait très largement autour, des volumes parus après mon adolescence et que je n’avais pas lus. C’est la raison pour laquelle j’ai englouti tous les romans du Cycle de Fondation en cet été 2025 avec un plaisir régressif certain.
Dans Terre et Fondation, paru en 1986 et que je n’avais pas lu à l’époque, les 3 personnages principaux sont persuadés qu’il existe une planète des origines de l’espèce humaine et partent à sa recherche. Leurs pérégrinations les conduisent sur une planète désertée depuis des milliers d’années, Melpomenia, sur laquelle ils découvrent, à même le mur d’un bâtiment officiel, une plaque gravée faisant la liste des 50 premiers mondes occupés par les humains et indiquant leurs « coordonnées galactiques ». L’un des personnage fait alors l’hypothèse que la conquête de ces mondes s’est opérée de manière symétrique dans toutes les directions d’un espace centré sur la planète des origines, ou sur son soleil, ce qui signifierait que les coordonnées obtenues doivent avoir pour enveloppe une quasi-sphère dont le centre serait la planète cherchée. Dans la mesure où ils ont, à ce moment du récit, déjà visité 3 de ces 50 planètes, ils estiment que leur ordinateur de bord — évidemment surpuissant — pourra extrapoler la position des 47 autres, corrigées des variations temporelles et en déduire le centre de gravité du nuage obtenu. Je m’entends alors penser « sans l’unité de mesure, ça va être chaud ! », ce à quoi le personnage ajoute immédiatement qu’il va parier sur une inertie historique de la science humaine selon laquelle les unités utilisées à l’époque, c’est à dire 20 000 ans plus tôt, sont toujours celles utilisées pour le voyage intersidéral.
Il n’en fallait pas plus pour aiguillonner ma curiosité et m’amener à me poser la question: est-il possible, à partir des coordonnées de 3 points de l’espace, de retrouver le centre du repère (supposé orthonormal) dans lequel elles sont produites ?
Hypothèses simplificatrices
Tout d’abord, simplifions le problème: ramenons-nous à deux points du plan $A$ et $B$. Si leurs coordonnées sont décimales, nous n’altérons pas la généralité en les multipliant par la plus petite puissance de 10 qui les rend toutes deux entières. À une translation près, nous pouvons faire en sorte que $A$ devienne l’origine puis si nécessaire, à une symétrie près, que $B$ soit situé dans le quadrant supérieur droit, ses coordonnées devenant finalement entières et positives.
Le problème devient: soit $a$ et $b$ deux entiers naturels et $B(a,b)$ dans le repère de centre $A$, sommes-nous capable de construire à la règle et au compas un triangle rectangle $ACB$, rectangle en $C$ donc d’hypoténuse $[AB]$ tel que $AC=a$ et $CB=b$ ?
Préalables de constructibilité
Nous n’allons pas ici réinventer l’eau chaude: les connaissances nécessaires en constructibilité sont expliquées beaucoup plus clairement que je ne pourrais le faire ici, par exemple dans cette excellente vidéo d’Exo7 1que je vous enjoins de regarder avant de continuer si vous n’êtes pas familier avec ces opérations.
Nous admettrons donc désormais que nous savons, à la règle et au compas et une fois une unité choisie: tracer la perpendiculaire à une droite passant par un point donné, tracer la parallèle à une droite passant par un point donné, multiplier une longueur par un entier donné, diviser un segment en parties de longueurs égales.
Télos
Une fois n’est pas coutume, commençons par la fin et admettons que les informations en notre possession nous ont permis de déterminer l’échelle dans laquelle nous sommes placés, c’est à dire l’unité dans laquelle les coordonnées initiales nous ont été fournies. Alors la construction du centre devient étonnamment simple comme nous allons le voir sur un exemple, illustré par la Figure 1 juste en dessous.
Soit les point $A(-0,3;0,4)$ et $B(0,1;-0,2)$ dans le repère que nous cherchons à obtenir. En multipliant toutes les coordonnées par 10 (c’est à dire en divisant l’unité obtenue par 10), nous obtenons $A(-3;4)$ et $B(1;-2)$.
Construisons le lieu des triangles rectangles d’hypoténuse $[AB]$ c’est à dire le cercle de diamètre $[AB]$.
La distance horizontale au sens du repère cherché est $\vert x_B-x_A\vert =\vert 1-(-3)\vert =4$ tandis que la distance verticale est $\vert y_B-y_A\vert=\vert -2-4\vert=6 $ et nous pouvons à l’aide de notre échelle construire un segment de longueur $4$ et un autre de longueur $6$.
Nous pouvons alors construire le cercle de centre $A$ et de rayon de longueur $6$ ou le cercle $B$ et de rayon de longueur $4$: ils se coupent tous trois en un point $H$ dont les coordonnées dans le repère cherché sont naturellement $H(-3;-2) $ puisque $H$ possède l’abscisse de $A$ et l’ordonnée de $B$.
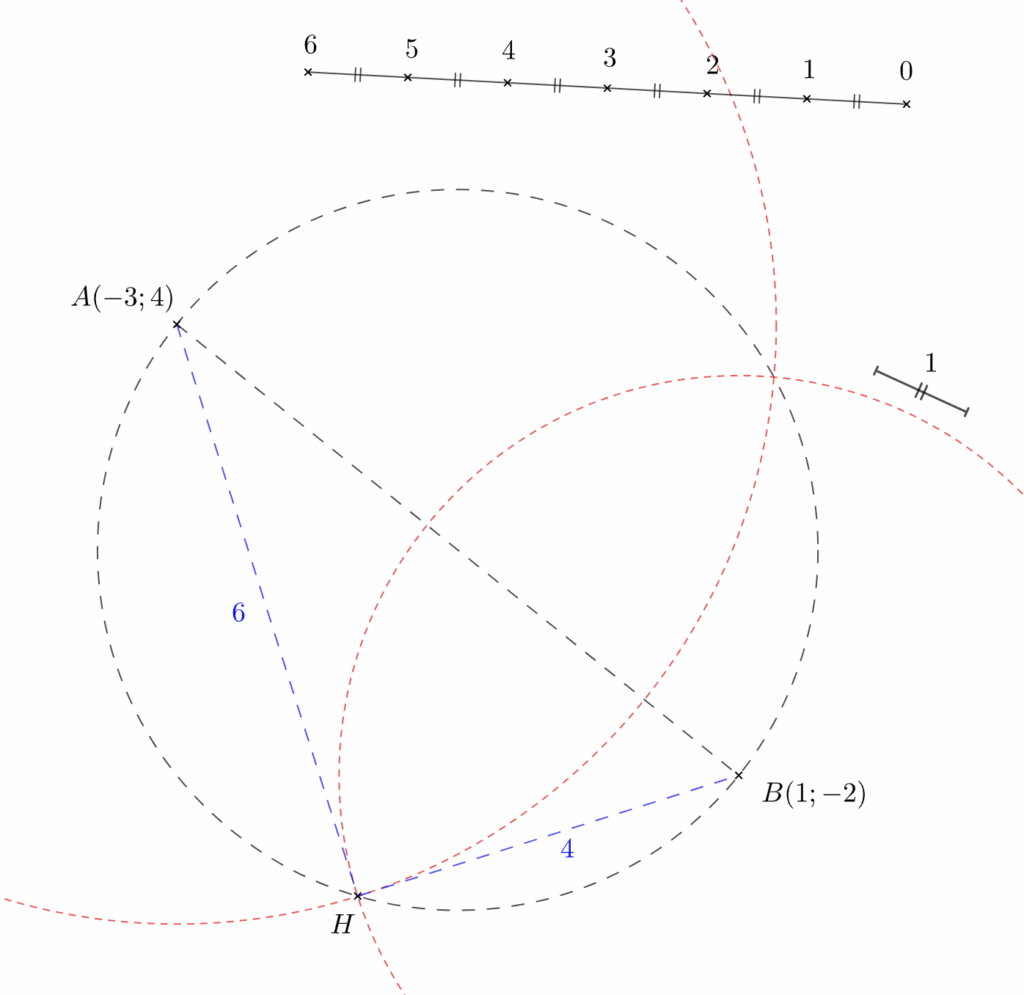
En opérant alors une translation de $H$ d’un vecteur $\vec v(3;2) $ suivant les côtés du triangle $AHB$, nous obtenons l’origine du repère cherché, intersection de deux axes que nous pouvons construire parallèlement aux côtés de $AHB$ et sur lesquels nous pouvons reporter la longueur unitaire, comme indiqué sur la figure 2 ci-dessous.
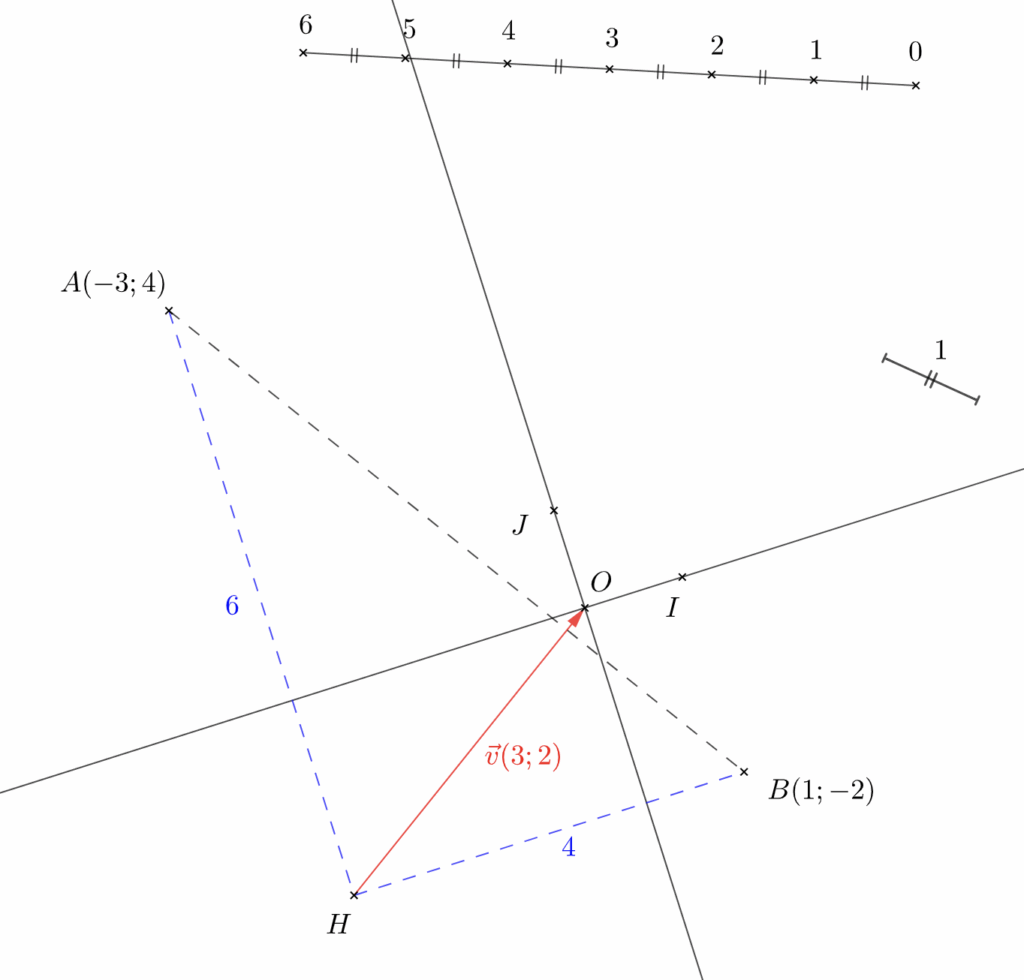
Notons donc qu’une fois obtenue la longueur unité, il est très simple de retrouver l’origine et de construite le repère à la règle et au compas.
Archí
Il nous reste donc à nous assurer de notre capacité à construire un segment unitaire à partir de la seule information en notre possession: la longueur du segment $[AB]$ fourni.
Évacuons immédiatement le cas trivial et rare d’une distance $AB=n$ déjà entière: il nous suffirait alors de diviser le segment $[AB]$ en $n$ segments qui seraient alors de longueur $1$ et nous pourrions conclure grâce au télos.
Le cas général est donc celui où $n$ n’est pas un carré parfait et donc d’une distance $AB$ radicale de type $\sqrt{n}$. Notons cependant car cela est très important, que $n$ est par construction la somme de deux carrés. Voici un exemple correspondant à la figure 3.
Soit les points $A(1;7)$ et $B(3;2)$. Nous avons alors $AB=\sqrt{(3-1)^2+(2-7)^2}=\sqrt{29}$
Donnons nous une échelle arbitraire et construisons un triangle rectangle $PQR$ rectangle en $Q$ tel que $PQ=5$ et $QR=2$, distances obtenues en calculant les différences des abscisses et des ordonnées de $A$ et de $B$..
Ainsi $PR=\sqrt{29}$.
Construisons maintenant une parallèle $(\Delta)$ à $(AB)$ et reportons notre distance $PR$ dessus sous la forme du segment $[A’B’]$. À l’intersection du cercle de centre $A’$ de rayon $5$ et du cercle de centre $B’$ de rayon $2$, nous avons le troisième sommet $H’$ du triangle rectangle $A’H’B’$, comme indiqué sur la figure ci-dessous où sont représentées en noir les données d’origine et en bleu les constructions à notre échelle arbitraire.
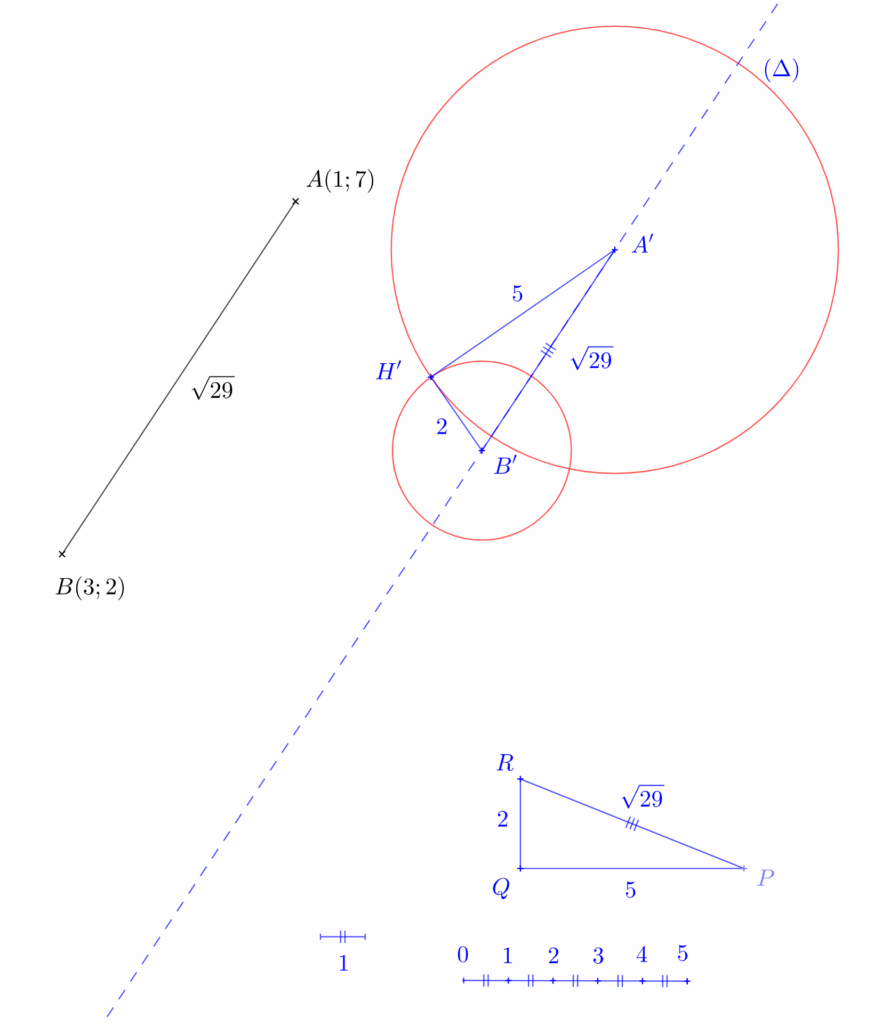
Il ne nous reste plus alors qu’à construire la parallèle à $(H’B’)$ passant par $B$ ainsi que la parallèle à $(H’A’)$ passant par $A$, toutes deux se coupant en $H$.
Enfin, nous diviserons le segment $[HB]$ en $2$ (ou le segment $[AH]$ en $5$) et nous obtiendrons l’échelle de la figure d’origine, ce qui en retournant au télos nous permettra de conclure, comme cela apparaît sur la figure 4 ci-dessous.
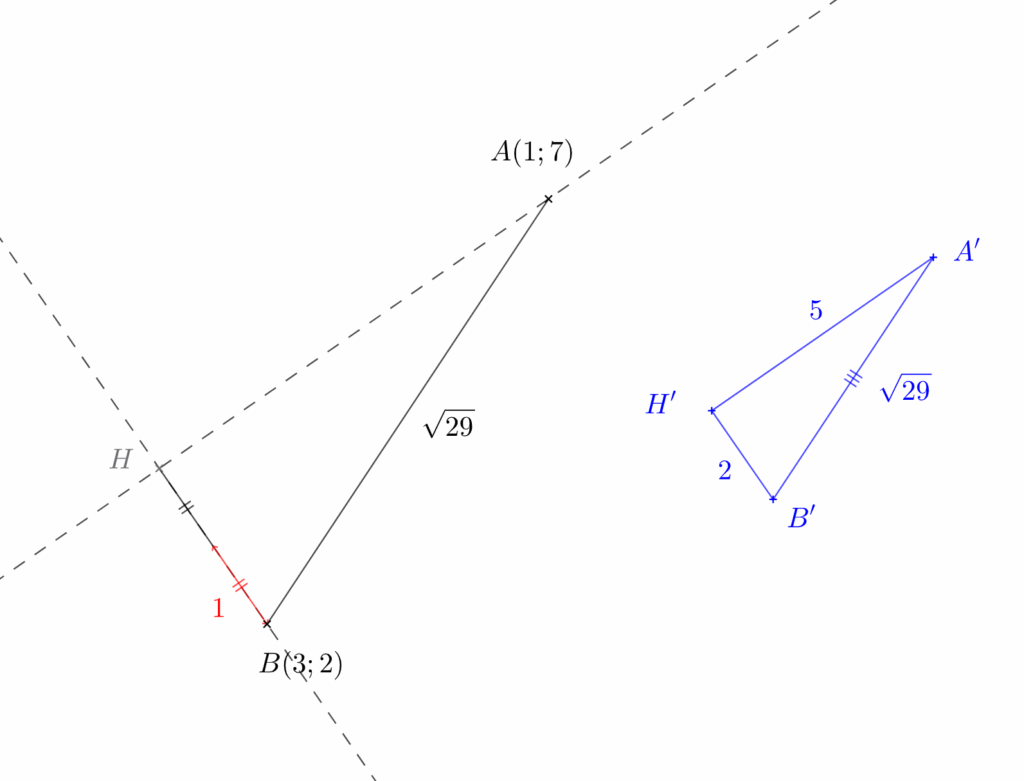
Conclusion
Il est donc bien possible, avec les outils géométriques fondamentaux, de retrouver l’origine et la norme d’un repère orthonormé du plan en ne connaissant que les coordonnées décimales de deux points donnés. Bien évidemment, le passage à la dimension 3 n’est pas fondamentalement plus compliqué en théorie, mais il nécessitera effectivement un outil numérique de représentation.
Une question demeure cependant: nous avons largement exploité le fait que $n$ s’écrive par construction comme la somme de deux carrés, mais serions-nous capable, même si cela n’est pas notre problème ici, de retrouver la longueur unité dans le cas où la longueur fournie serait la racine d’un nombre qui n’est pas la somme de deux carrés ? Si vous avez la solution, n’hésitez pas à la donner en commentaires ! (Attention: vous devez-vous inscrire pour commenter)
Notes de bas de page
- Vous pouvez également regarder cette seconde vidéo, beaucoup plus théorique et moins utile pour nous ici, mais également très intéressante si vous aimez les mathématiques.
